| 把一质量M的物质快速上下运动,此时上下移动所受之阻力,不是来自弹簧而是质量M本身 |
| 的惯性;假设质量上下移动的幅度为A,频率为f 周波/秒,此质量必依正弦波动亦称(谐 |
| 和振动)方式上下抖动,以数学式表示如下: |
|
|
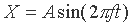 |
| X:由中心点往上或下之移动距离 |
| A:最大振幅 |
| |
| 因此克服来自弹簧刚度的力量为Fs(弹簧)=KX=Kasin(2πft) K= 弹簧刚度 |
| 而质量M上下运动所产生的惯性力量为质量M乘上加速度A即得: |
| |
| 负号代表惯性力与弹簧力呈反方向作用,也就是弹簧力量在运动抵达谷底时,必定把质量M往 |
| 上推举到静止时位置;但是运动的惯性却继续把质量M往上推至冲程的顶点。来自惯性的运 |
| 动阻力与运动之频率成正比,频率越高惯性力越大;但是不管频率的高低,弹簧的力量都是 |
| 不变。因此这两个反方向的力在某一特定的运动频率时,会相互平衡抵消;在理论上当质量 |
| M在此频率运动时,无须借助任何力量,即可产生很大位移,除非有磨擦阻力或其它阻尼力 |
| 量来牵制其自由运动。这特定频率我们称它为此系统的自然频率(Natural Frequency )。 |
| |
| 如果弹簧力与惯性力互相抵消则Fs=F |
| Fs(弹簧)+F(惯性 )=0 |
|
| |
| 如果此时系统之自然频率与弹簧之自然频率相吻合,则此系统必定会以极大之振幅上下激烈 |
| 振荡,这种现象我们称之为共振(Resonance)。 |
| |

