| 把一質量M的物質快速上下運動,此時上下移動所受之阻力,不是來自彈簧而是質量M本身 |
| 的慣性;假設質量上下移動的幅度為A,頻率為f 週波/秒,此質量必依正弦波動亦稱(諧 |
| 和振動)方式上下抖動,以數學式表示如下: |
|
|
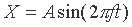 |
| X:由中心點往上或下之移動距離 |
| A:最大振幅 |
| |
| 因此克服來自彈簧剛度的力量為Fs(彈簧)=KX=Kasin(2πft) K= 彈簧剛度 |
| 而質量M上下運動所產生的慣性力量為質量M乘上加速度A即得: |
| |
| 負號代表慣性力與彈簧力呈反方向作用,也就是彈簧力量在運動抵達谷底時,必定把質量M往 |
| 上推舉到靜止時位置;但是運動的慣性卻繼續把質量M往上推至衝程的頂點。來自慣性的運 |
| 動阻力與運動之頻率成正比,頻率越高慣性力越大;但是不管頻率的高低,彈簧的力量都是 |
| 不變。因此這兩個反方向的力在某一特定的運動頻率時,會相互平衡抵消;在理論上當質量 |
| M在此頻率運動時,無須借助任何力量,即可產生很大位移,除非有磨擦阻力或其它阻尼力 |
| 量來牽制其自由運動。這特定頻率我們稱它為此系統的自然頻率(Natural Frequency )。 |
| |
| 如果彈簧力與慣性力互相抵消則Fs=F |
| Fs(彈簧)+F(慣性 )=0 |
|
| |
| 如果此時系統之自然頻率與彈簧之自然頻率相吻合,則此系統必定會以極大之振幅上下激烈 |
| 振盪,這種現象我們稱之為共振(Resonance)。 |
| |

